Fully homomorphic encryption: Construction

In the last lecture we defined fully homomorphic encryption, and showed the “bootstrapping theorem” that transforms a partially homomorphic encryption scheme into a fully homomorphic encryption, as long as the original scheme can homomorphically evaluate its own decryption circuit. In this lecture we will show an encryption scheme (due to Gentry, Sahai and Waters, henceforth GSW) meeting the latter property. That is, this lecture is devoted to proving¹ the following theorem:

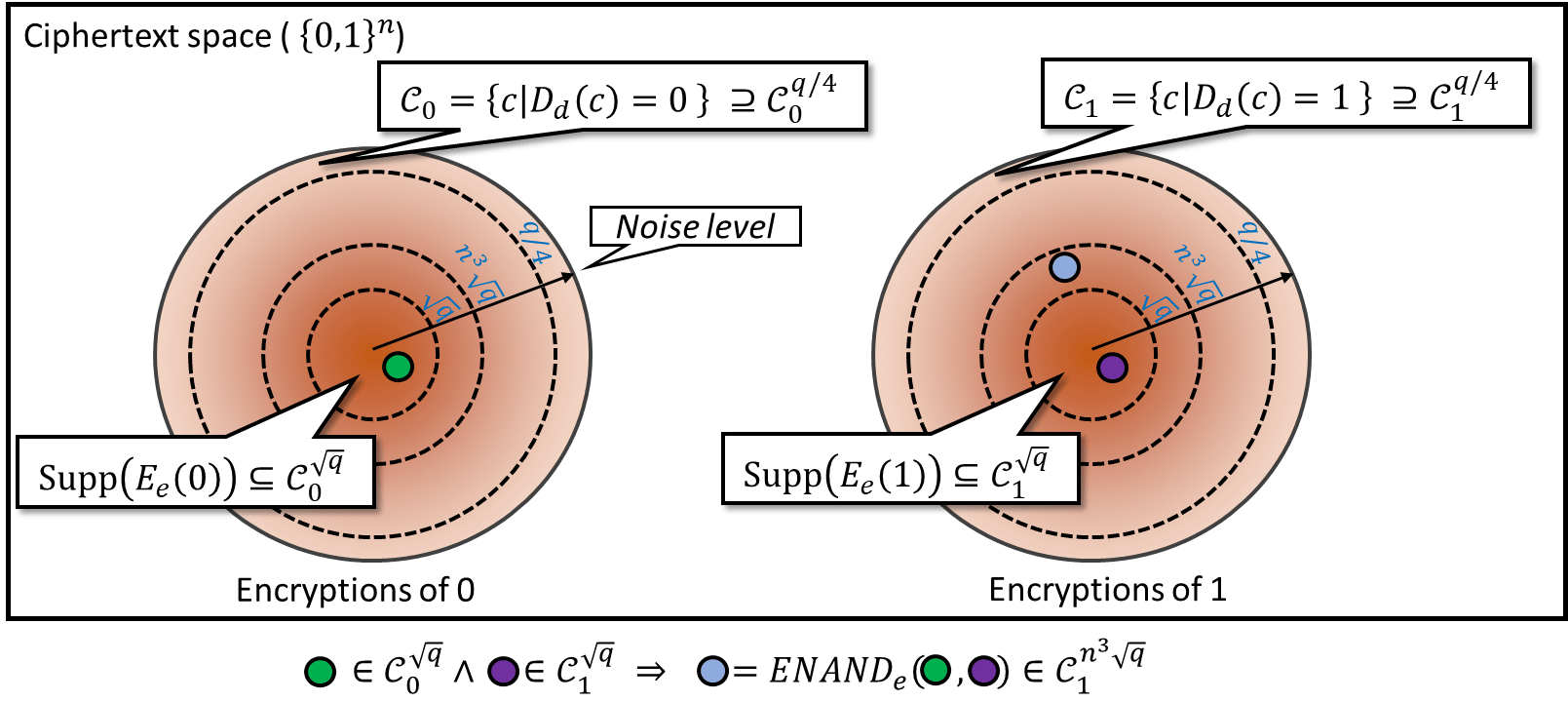
Before the detailed description and analysis, let us first outline our strategy. The following notion of “noisy homomorphic encryption” will be of essential importance (see also Figure 15.1).

The noisy homomorphic encryption actually states that if \(C\) and \(C'\) encrypt \(b\) and \(b'\) up to error \(\eta\) and \(\eta'\), respectively, then \(\ensuremath{\mathit{ENAND}}(c,c')\) encrypts \(\ensuremath{\mathit{NAND}}(b,b')\) up to some error which can be controlled by \(\eta,\eta'\). The coefficient \(n^3\) is not essential here; we just need the order \(poly(n)\). This property allows us to perform the \(\ensuremath{\mathit{ENAND}}\) operator repeatly as long as we can guarantee the accumulated error is smaller than \(q/4\), which means that the decryption can be done correctly. The next theorem tells us with what depth a circuit can be computed homomorphically.

We will assume the LWE conjecture with \(q(n) \approx 2^{\sqrt{n}}\) in the remainder of this chapter. With Theorem 15.3 in hand, our goal is to construct a noisy FHE such that the decryption map (specifically the map \(d \mapsto D_d(c)\) for any fixed ciphertext \(c\)) can be computed by a circuit with depth at most \(polylog(n)\). (Theorem 14.8 refers to the map \(d \mapsto \neg(D_d(c) \wedge D_d(c'))\), but this latter map is obtained by applying one more NAND gate to two parallel executions of \(d \mapsto D_d(c)\), and hence if the map \(d \mapsto D_d(c)\) has depth at most \(polylog(n)\) then so does the map \(d \mapsto \neg(D_d(c) \wedge D_d(c'))\).) Once we do this then we can obtain a fully homomorphic encryption scheme. We will head into some details show how to construct things we want in the rest of this chapter. The most technical and interesting part would be how to upper bound the noise/error.

Prelude: from vectors to matrices

In the linear homomorphic scheme we saw in the last lecture, every ciphertext was a vector \(c\in\Z_q^n\) such that \(\langle c,s \rangle\) equals (up to scaling by \(\floor{\tfrac{q}{2}}\)) the plaintext bit. We saw that adding two ciphertexts modulo \(q\) corresponded to XOR’ing (i.e., adding modulo \(2\)) the corresponding two plaintexts. That is, if we define \(c \oplus c'\) as \(c+c' \pmod{q}\) then performing the \(\oplus\) operation on the ciphertexts corresponds to adding modulo \(2\) the plaintexts.

However, to get to a fully, or even partially, homomorphic scheme, we need to find a way to perform the NAND operation on the two plaintexts. The challenge is that it seems that to do that we need to find a way to evaluate multiplications: find a way to define some operation \(\otimes\) on ciphertexts that corresponds to multiplying the plaintexts. Alas, a priori, there doesn’t seem to be a natural way to multiply two vectors.

The GSW approach to handle this is to move from vectors to matrices. As usual, it is instructive to first consider the cryptographer’s dream world where Gaussian elimination doesn’t exist. In this case, the GSW ciphertext encrypting \(b\in\{0,1\}\) would be an \(n\times n\) matrix \(C\) over \(\Z_q\) such that \(Cs = bs\) where \(s\in\Z_q^n\) is the secret key. That is, the encryption of a bit \(b\) is a matrix \(C\) such that the secret key is an eigenvector (modulo \(q\)) of \(C\) with corresponding eigenvalue \(b\). (We defer discussion of how the encrypting party generates such a ciphertext, since this is in any case only a “dream” toy example.)

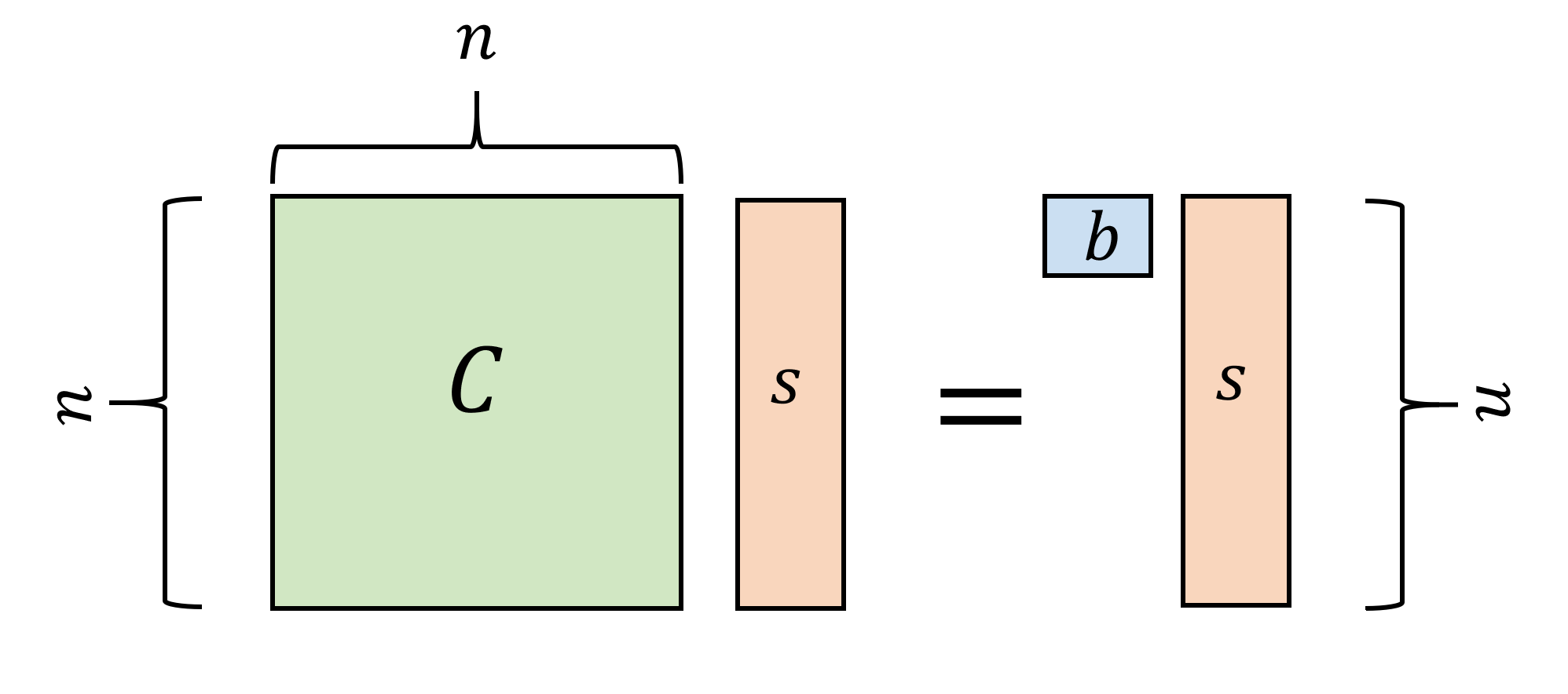
Given \(C\) and \(s\) we can recover \(b\) by just checking if \(Cs=s\) or \(Cs=0^n\). The scheme allows homomorphic evaluation of both addition (modulo \(q\)) and multiplication, since if \(Cs = bs\) and \(C's=b's\) then we can define \(C \oplus C' = C + C'\) (where on the righthand side, addition is simply done in \(\Z_q\)) and \(C\otimes C' = \ensuremath{\mathit{CC}}'\) (where again this refers to matrix multiplication in \(\Z_q\)).

Indeed, one can verify that both addition and multiplication succeed since

Addition modulo \(q\) is not the same as XOR, but given these multiplication and addition operations, we can implement the NAND operation as well. Specifically, for every \(b,b' \in \{0,1\}\), \(b \; \ensuremath{\mathit{NAND}} \; b' = 1-bb'\). Hence we can take a ciphertext \(C\) encrypting \(b\) and a ciphertext \(C'\) encrypting \(b'\) and transform these two ciphertexts to the ciphertext \(C''=(I-CC')\) that encrypts \(b\; \ensuremath{\mathit{NAND}} \; b'\) (where \(I\) is the identity matrix). Thus in a world without Gaussian elimination it is not hard to get a fully homomorphic encryption.

Real world partially homomorphic encryption

We now discuss how we can obtain an encryption in the real world where, as much as we’d like to ignore it, there are people who walk among us (not to mention some computer programs) that actually know how to invert matrices. As usual, the idea is to “fool Gaussian elimination with noise” but we will see that we have to be much more careful about “noise management”, otherwise even for the party holding the secret key the noise will overwhelm the signal.²

The main idea is that we can expect the following problem to be hard for a random secret \(s\in\Z_q^n\): distinguish between samples of random matrices \(C\) and matrices where \(Cs = bs + e\) for some \(b\in\{0,1\}\) and “short” \(e\) satisfying \(|e_i| \leq \sqrt{q}\) for all \(i\). This yields a natural candidate for an encryption scheme where we encrypt \(b\) by a matrix \(C\) satisfying \(Cs = bs + e\) where \(e\) is a “short” vector.³

We can now try to check what adding and multiplying two matrices does to the noise. If \(Cs = bs+e\) and \(C's=b's+e'\) then

We would have loved to say that we can define as above \(C\oplus C' = C+C' \pmod q\) and \(C\otimes C' = \ensuremath{\mathit{CC}}'\pmod q\). For this we would need that the vector \((C+C')s\) equals \((b+b')s\) plus a “short” vector and the vector \(\ensuremath{\mathit{CC}}'s\) equals \(bb's\) plus a “short” vector. The former statement indeed holds. Looking at Equation 15.2 we see that \((C+C')s\) equals \((b+b')s\) up to the “noise” vector \(e+e'\), and if \(e,e'\) are “short” then \(e+e'\) is not too long either. That is, if \(|e_i|<\eta\) and \(|e'_i|<\eta'\) for every \(i\) then \(|e_i+e'_i|<\eta + \eta'\). So we can at least handle a significant number of additions before the noise gets out of hand.

However, if we consider Equation 15.2, we see that \(\ensuremath{\mathit{CC}}'\) will be equal to \(bb's\) plus the “noise vector” \(b'e + Ce'\). The first component \(b'e\) of this noise vector is “short” (after all \(b'\in \{0,1\}\) and \(e\) is “short”). However, the second component \(Ce'\) could be a very large vector. Indeed, since \(C\) looks like a random matrix in \(\Z_q\), no matter how small the entries of \(e'\), many of the entries of \(Ce'\) will be large. Hence multiplying \(e'\) by \(C\) takes us “beyond the edge of chaos” and makes the noise too large for decryption to be successful.

Noise management via encoding

The problem we had above is that the entries of \(C\) are elements in \(\Z_q\) that can be very large, while we would have loved them to be small numbers such as \(0\) or \(1\). At this point one could say

“If only there was some way to encode numbers between \(0\) and \(q-1\) using only \(0\)’s and \(1\)’s”

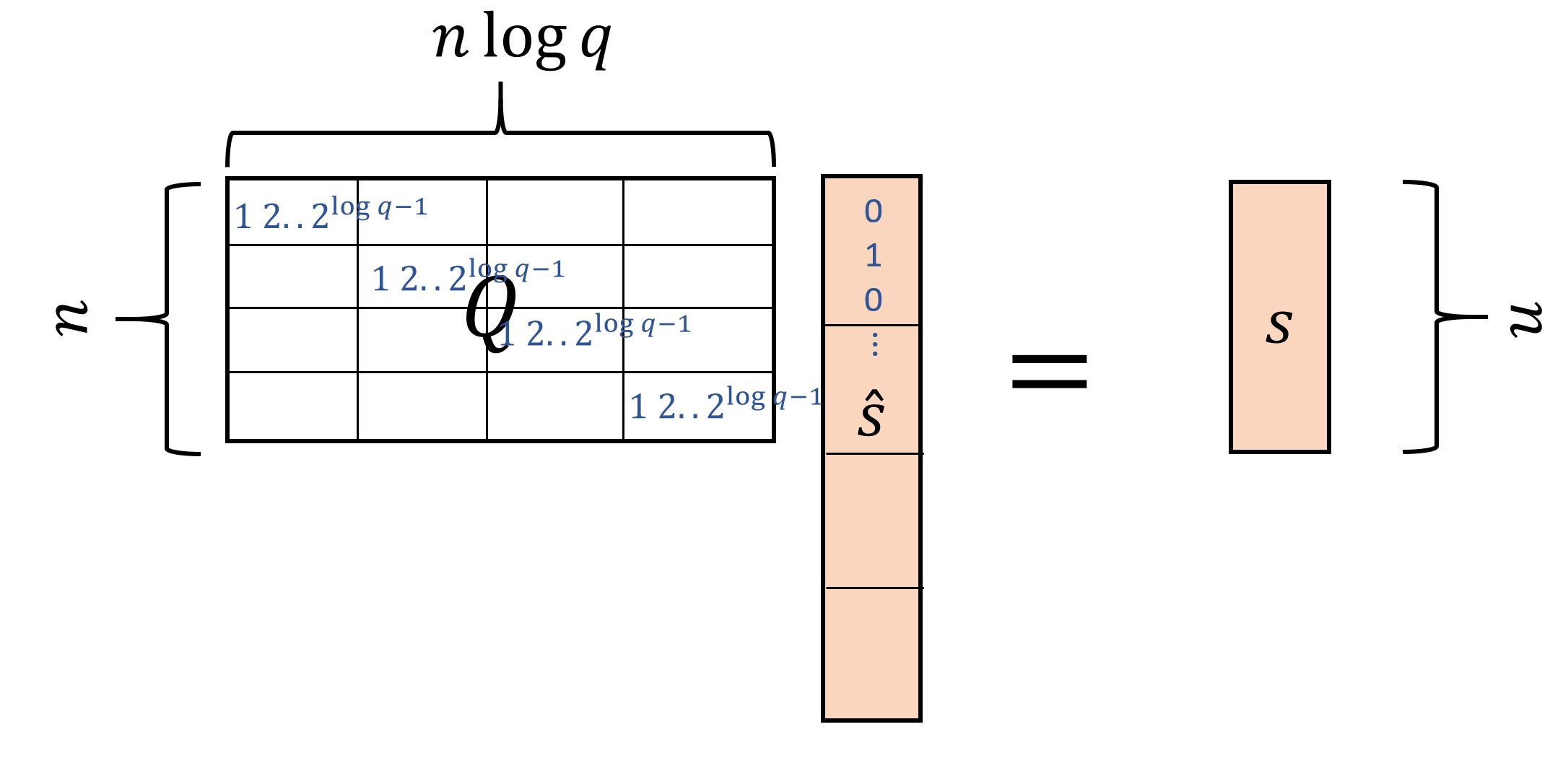
If you think about it hard enough, it turns out that there is something known as the “binary basis” that allows us to encode a number \(x\in\Z_q\) as a vector \(\hat{x}\in\{0,1\}^{\log q}\).⁴ What’s even more surprising is that this seemingly trivial trick turns out to be immensely useful. We will define the binary encoding of a vector or matrix \(x\) over \(\Z_q\) by \(\hat{x}\). That is, \(\hat{x}\) is obtained by replacing every coordinate \(x_i\) with \(\log q\) coordinates \(x_{i,0},\ldots,x_{i,\log q-1}\) such that

Specifically, if \(s\in \Z_q^n\), then we denote by \(\hat{s}\) the \(n\log q\)-dimensional vector with entries in \(\{0,1\}\), such that each \(\log q\)-sized block of \(\hat{s}\) encodes a coordinate of \(s\). Similarly, if \(C\) is an \(m\times n\) matrix, then we denote by \(\hat{C}\) the \(m\times n\log q\) matrix with entries in \(\{0,1\}\) that corresponds to encoding every \(n\)-dimensional row of \(C\) by an \(n\log q\)-dimensional row where each \(\log q\)-sized block corresponds to a single entry. (We still think of the entries of these vectors and matrices as elements of \(\Z_q\) and so all calculations are still done modulo \(q\).)

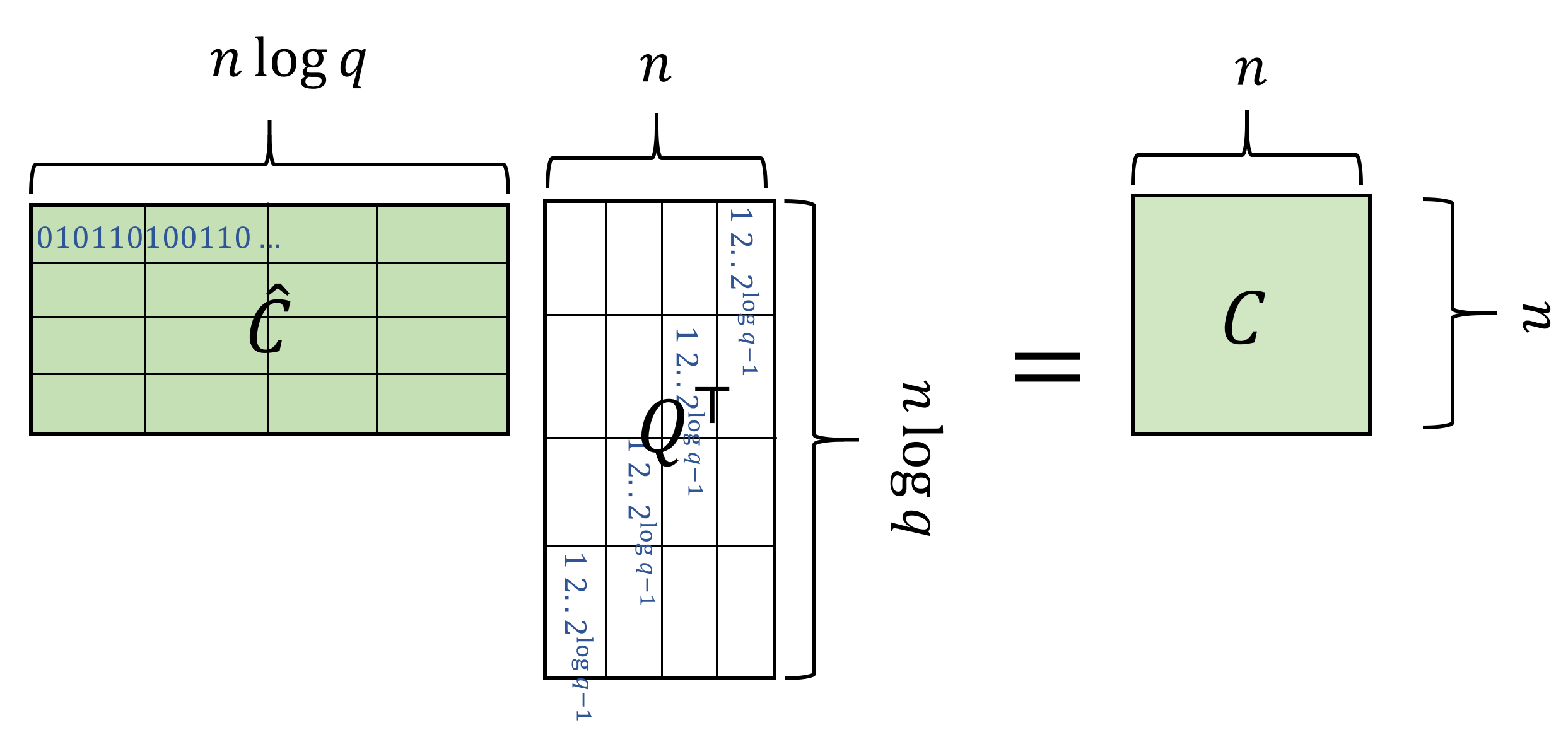
While encoding in the binary basis is not a linear operation, the decoding operation is linear as one can see in Equation 15.3. We let \(Q\) be the \(n \times (n\log q)\) “decoding” matrix that maps an encoding vector \(\hat{s}\) back to the original vector \(s\). Specifically, every row of \(Q\) is composed of \(n\) blocks each of \(\log q\) size, where the \(i\)-th row has only the \(i\)-th block nonzero, and equal to the values \((1,2,4,\ldots,2^{\log q-1})\). It’s a good exercise to verify that for every vector \(s\in \Z_q^n\) and matrix \(C\in \Z_q^{n\times n}\), \(Q\hat{s}=s\) and \(\hat{C}Q^\top =C\). (See Figure 15.3 amd Figure 15.4.)

Our final encryption scheme: We describe below the key generation, encryption and decryption algorithms of our final homomorphic encryption scheme (FHEENC). It will satisfy the following properties:

1. Ciphertexts are \((n \log q)\times (n\log q)\) matrices \(C\) with all coefficients in \(\{0,1\}\).

2. The secret key is a vector \(s \in \Z_q^n\). We let \(v \in \Z_q^{n \log q}\) be the vector \(V = Q^\top s\).

3. An encryption of \(b\in \{0,1\}\) is a matrix \(C\) satisfying the following “ciphertext equation”

   \[Cv =bv + e \;\;(15.4)\]
   for a “short” \(e\).

Given the conditions 1,2, and 3, we can now define the addition and multiplication operations for two ciphertexts \(C,C'\) as follows:

• \(C \oplus C' = C + C' \pmod{q}\)

• \(C \otimes C' = \widehat{(\ensuremath{\mathit{CQ}}^\top)}C'\)

Correctness of operations. Suppose that \(Cv = bv + e\) and \(C'v = b'v + e'\). Then

which means that \(C \oplus C'\) satisfies the ciphertext equation Equation 15.4 with respect to the plaintext \(b+b'\), with the short vector \(e+e'\).

Let’s now analyze the more challenging case of \(C \otimes C'\).

But since \(v=Q^\top s\) and \(\hat{A}Q^\top = A\) for every matrix \(A\), the righthand side of Equation 15.6 equals

but since \(\widehat{B}\) is a matrix with small coefficients for every \(B\) and \(e'\) is short, the righthand side of Equation 15.7 equals \(b'Cv\) up to a short vector, and since \(Cv=bv+e\) and \(b'e\) is short, we get that \((C\otimes C')v\) equals \(b'bv\) plus a short vector as desired.

We can now define

Keeping track of parameters. For \(C\) that encrypts a plaintext \(b\), let \(\eta(C) = \max_{i\in [n]} |Cv -bv|\). Now if we can see that if \(C\) encrypts \(b\) with noise \(\eta(C)\) and \(C'\) encrypts \(b'\) with noise \(\eta(C')\), then \(\ensuremath{\mathit{ENAND}}(C,C')\) will encrypt \(1-bb' = \ensuremath{\mathit{NAND}}(b,b')\) with noise of magnitude at most \(O(\mu + n\log q \mu')\), which is smaller than \(n^3\cdot \max\{\eta(C),\eta(C')\}\) for \(q\approx 2^{\sqrt{n}}\).

Putting it all together

We now describe the full scheme. We are going to use a quantitatively stronger version of LWE. Namely, the \(q(n)\)-dLWE assumption for \(q(n)=2^{\sqrt{n}}\). It is not hard to show that we can relax our assumption to \(q(n)\)-LWE \(q(n)=2^{polylog(n)}\) and Brakerski and Vaikuntanathan showed how to relax the assumption to standard (i.e. \(q(n)=poly(n)\)) LWE though we will not present this here.

FHEENC:

• Key generation: As in the scheme of last lecture the secret key is \(s\in\Z_q^n\) and the public key is a generator \(G_s\) such that samples from \(G_s(1^n)\) are indistinguishable from independent random samples from \(\Z_q^n\) but if \(c\) is output by \(G_s\) then \(|\langle c,s \rangle|<\sqrt{q}\), where the inner product (as all other computations) is done modulo \(q\) and for every \(x\in\Z_q=\{0,\ldots,q-1\}\) we define \(|x|=\min \{ x, q-x \}\). As before, we can assume that \(s_1 = \floor{q/2}\) which implies that \((Q^\top s)_1\) is also \(\floor{q/2}\) since (as can be verified by direct inspection) the first row of \(Q^\top\) is \((1,0,\ldots,0)\).

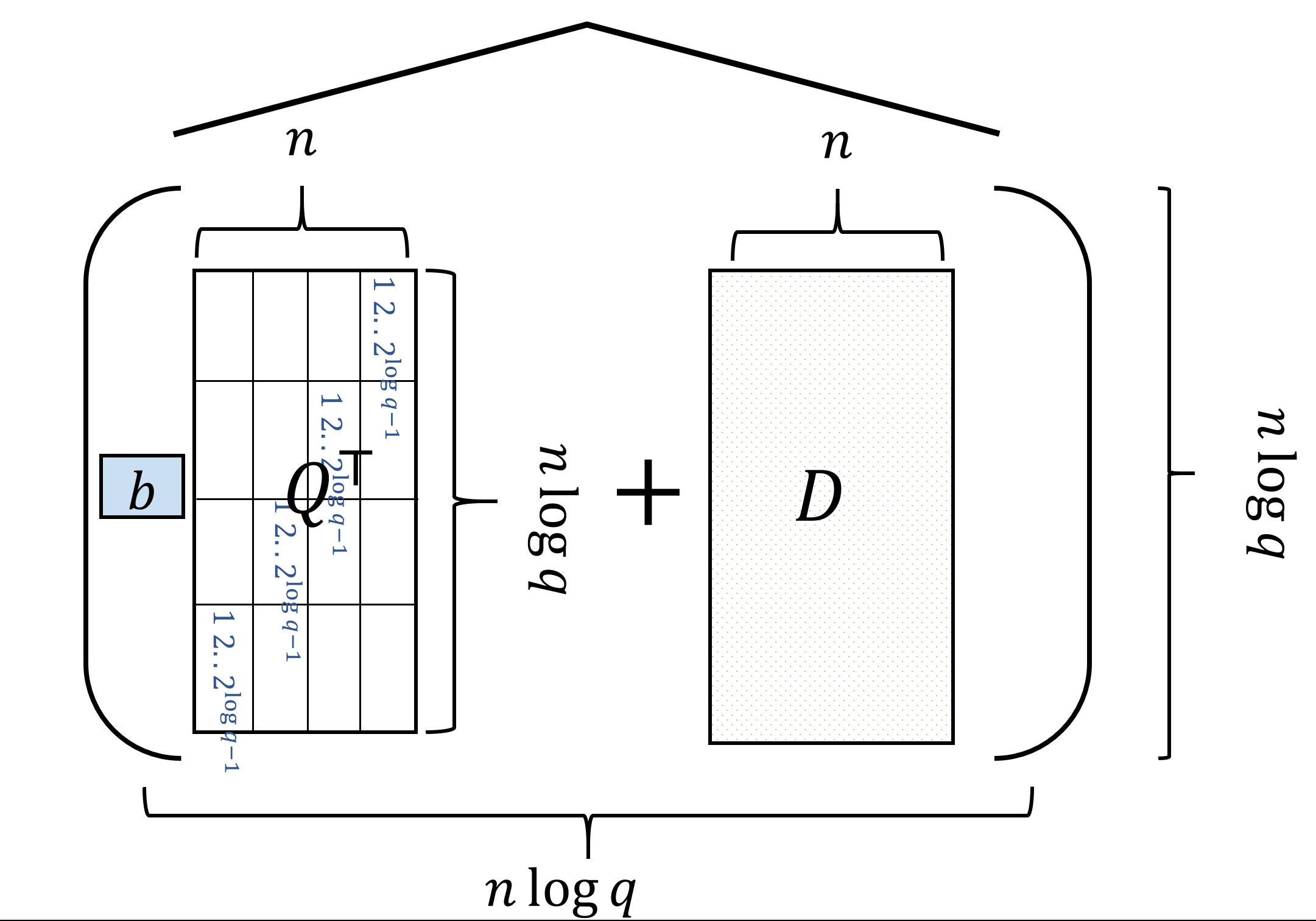
• Encryption: To encrypt \(b\in\{0,1\}\), let \(d_1,\ldots,d_{n\log q} \leftarrow_R G_s(1^n)\) output \(C=\widehat{(bQ^\top +D)}\) where \(D\) is the matrix whose rows are \(d_1,\ldots,d_{n\log q}\) generated from \(G_s\). (See Figure 15.5)

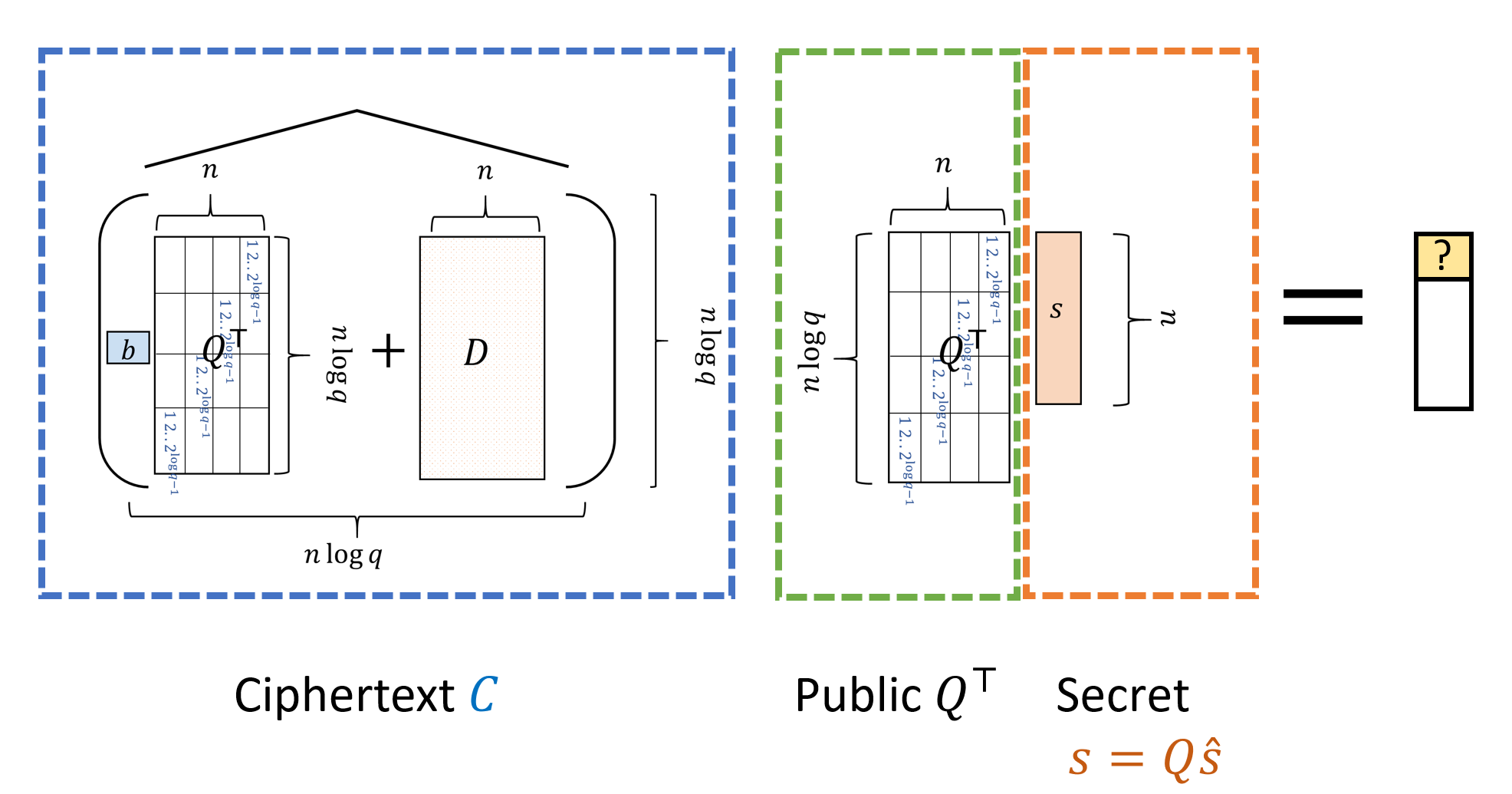
• Decryption: To decrypt the ciphertext \(C\), we output \(0\) if \(|(\ensuremath{\mathit{CQ}}^\top s)_1|<0.1q\) and output \(1\) if \(0.6q>|(\ensuremath{\mathit{CQ}}^\top s)_1|>0.4q\), see Figure 15.6. (It doesn’t matter what we output on other cases.)

• NAND evaluation: Given ciphertexts \(C,C'\), we define \(C \overline{\wedge} C'\) (sometimes also denoted as \(\ensuremath{\mathit{NANDEVAL}}(C,C')\)) to equal \(I- \widehat{(\ensuremath{\mathit{CQ}}^\top)}C'\), where \(I\) is the \((n\log q)\times (n\log q)\) identity matrix.

Analysis of our scheme

To show that that this scheme is a valid partially homomorphic scheme we need to show the following properties:

1. Correctness: The decryption of an encryption of \(b\in\{0,1\}\) equals \(b\).

2. CPA security: An encryption of \(0\) is computationally indistinguishable from an encryption of \(1\) to someone that got the public key.

3. Homomorphism: If \(C\) encrypts \(b\) and \(C'\) encrypts \(b'\) then \(C \overline{\wedge} C'\) encrypts \(b\; \ensuremath{\mathit{NAND}}\; b'\) (with a higher amount of noise). The growth of the noise will be the reason that we will not get immediately a fully homomorphic encryption.

4. Shallow decryption circuit: To plug this scheme into the bootstrapping theorem we will need to show that its decryption algorithm (or more accurately, the function in the statement of the bootstrapping theorem) can be evaluated in depth \(polylog(n)\) (independently of \(q\)), and that moreover, the noise grows slowly enough that our scheme is homomorphic with respect to such circuits.

Once we obtain 1-4 above, we can plug FHEENC into the Bootstrapping Theorem (Theorem 14.8) and thus complete the proof of existence of a fully homomorphic encryption scheme. We now address those points one by one.

Correctness

Correctness of the scheme will follow from the following stronger condition:

Lemma 15.5 implies correctness of decryption since by construction we ensured that \((Q^\top s)_1 \in (0.499q,0.5001q)\) and hence we get that if \(b=0\) then \(|(Cv)_1|=o(q)\) and if \(b=1\) then \(0.499q-o(q) \leq |(C_v)_1| \leq 0.501q + o(q)\).

CPA Security

To show CPA security we need to show that an encryption of \(0\) is indistinguishable from an encryption of \(1\). However, by the security of the trapdoor generator, an encryption of \(b\) computed according to our algorithm will be indistinguishable from an encryption of \(b\) obtained when the matrix \(D\) is a random \((n\log q)\times n\) matrix. Now in this case the encryption is obtained by applying the \(\hat{\cdot}\) operation to \(bQ^\top +D\) but if \(D\) is uniformly random then for every choice of \(b\), \(bQ^\top + D\) is uniformly random (since a fixed matrix plus a random matrix yields a random matrix) and hence the matrix \(bQ^\top + D\) (and so also the matrix \(\widehat{bQ^\top+D}\)) contains no information about \(b\). This completes the proof of CPA security (can you see why?).

If we want to plug in this scheme in the bootstrapping theorem, then we will also assume that it is circular secure. It seems a reasonable assumption though unfortuantely at the moment we do not know how to derive it from LWE. (If we don’t want to make this assumption we can still obtained a leveled fully homomorphic encryption as discussed in the previous lecture.)

Homomorphism

Let \(v=Q^\top s\), \(b\in\{0,1\}\) and \(C\) be a ciphertext such that \(Cv = bv + e\). We define the noise of \(C\), denoted as \(\mu(C)\) to be the maximum of \(|e_i|\) over all \(i\in[n\log q]\). We make the following lemma, which we’ll call the “noisy homomorphism lemma”:

Shallow decryption circuit

Recall that to plug in our homomorphic encryption scheme into the bootstrapping theorem, we needed to show that for every ciphertext \(C\) (generated by the encryption algorithm) the function \(f_C:\{0,1\}^{n \log q} \rightarrow \{0,1\}\) can be computed by a circuit of sufficiently shallow, where \(f_C\) is defined as

In our case a circuit of \(polylog(n) \ll n^5\) will be “sufficiently shallow”. Specifically, by repeatedly applying the noisy homomorphism lemma (Lemma 15.6), we can show that can homorphically evaluate every circuit of NAND gates whose depth \(\ell\) satisfies the condition \((2n\log q)^\ell \ll q\). If \(q = 2^{\sqrt{n}}\) then (assuming \(n\) is sufficiently large) as long as \(\ell < n^{0.49}\) this will be satisfied.

We will encode the secret key of the encryption scheme as the binary string \(\hat{s}\) which describes our vector \(s \in Z_q^n\) as a bit string of length \(n\log q\). Given a ciphertext \(C\), the decryption algorithm takes the dot product modulo \(q\) of \(s\) with the first row of \(\ensuremath{\mathit{CQ}}^\top\). This can be equivalently described as taking the dot product of \(\hat{s}\) with the first row of \(\ensuremath{\mathit{CQ}}^\top Q\). Decryption outputs \(0\) (respectively \(1\)) if the resulting number is small (respectively large).

In particular to show that \(f_C(\cdot)\) can be homomorphically evaluated it will suffice to show that for every fixed vector \(c\in \Z_q^{n\log q}\) there is a \(polylog(n) \ll n^{0.49}\) depth circuit \(F\) that on input a string \(\hat{s}\in\{0,1\}^{n \log q}\) will output \(0\) if \(|\langle c,\hat{s \rangle}| < q/10\) and output \(1\) if \(|\langle c,\hat{s \rangle}| > q/5\). (We don’t care what \(F\) does otherwise.) The above suffices since given a ciphertext \(C\) we can use \(F\) with the vector \(c\) being the top row of \(\ensuremath{\mathit{CQ}}^\top Q\), and hence \(\langle c,\hat{s} \rangle\) would correspond to the first entry of \(\ensuremath{\mathit{CQ}}^\top s\).

If \(c=(c_1,\ldots,c_{n\log q})\) is a vector then to compute its inner product with a \(0/1\) vector \(\hat{s}\) we simply need to sum up the numbers \(c_i\) where \(\hat{s}_i=1\). Summing up \(m\) numbers can be done via the obvious recursion in depth that is \(\log m\) times the depth for a single addition of two numbers. However, the naive way to add two numbers in \(\Z_q\) (each represented by \(\log q\) bits) will have depth \(O(\log q)\) which is too much for us. The issue is that while \(m = n\log q\) is polynomial in \(n\), \(q\) itself has exponential magnitude. In particular \(\log q \approx \sqrt{n}\), and we cannot afford to use a circuit of that depth.

Fortunately, because we only care about accuracy up to \(q/10\), we can make the calculation “shallower”. Specifically, if we add \(m\) numbers in \(\Z_q\) (each represented by \(\log q\) bits), we can drop all but the first \(100\log m\) most significant digits of our numbers. The reason is that dropping this can change each number by at most \((q/m^{100})\), and so if we ignore these digits, then it would change the sum of the \(m\) numbers by at most \(m(q/m^{100}) \ll q\). Hence we can easily do this work in \(poly(\log m)\) depth, which is \(poly(\log n)\) since \(m=poly(n)\).

Let us now show this more formally:

::: {.proof data-ref=“decdepthlem”} For every number \(x\in\Z_q\), define \(\tilde{x}\) to be the number that is obtained by writing \(x\) in the binary basis and setting all digits except the \(10\log m\) most significant ones to zero. Note that \(\tilde{x} \leq x \leq \tilde{x} + q/m^{10}\). The idea is that we will do the calculation by changing every number \(c_i\) and the modulos \(q\) into their correponding numbers \(\tilde{c}_i\) and \(\tilde{q}\).

We define \(f(\hat{s})\) to equal \(1\) if \(|\sum \hat{s}_i \tilde{c}_i \pmod {\tilde{q}}| \geq 0.3\tilde{q}\) and to equal \(0\) otherwise (where as usual the absolute value of \(x\) modulo \(\tilde{q}\) is the minimum of \(x\) and \(\tilde{q}-x\).) All numbers involved have zeroes in all but the \(10\log m\) most significant digits and so these less significant digits can be ignored. Hence we can add any pair of such numbers modulo \(\tilde{q}\) in depth \(O(\log m)^2\) using the standard elementary school algorithm to add two \(\ell\)-digit numbers in \(O(\ell^2)\) steps.

Now we can add the \(m\) numbers by adding pairs, and then adding up the results, and this way in a binary tree of depth \(\log m\) to get a total depth of \(O(\log m)^3\). So, all that is left to prove is that this function \(f\) satisfies the conditions (1) and (2).

If we look at the non modular sum then \(|\sum \hat{s}_i \tilde{c}_i - \sum \hat{s}_i c_i | < mq/m^{10} = q/m^9\) so now we want to show that the effect of taking modulo \(\tilde{q}\) is not much different from taking modulo \(q\). Indeed, note that this sum (before a modular reduction) is an integer between \(0\) and \(qm\). If \(x\) is such an integer and we divide \(x\) by \(q\) to write \(x = kq+ r\) for \(r<q\), then since \(x<qm\), \(k<m\), and so we can write \(x = k\tilde{q} + k(q-\tilde{q})+r\) so the difference between \(k \mod q\) and \(k \mod{\tilde{q}}\) will be (in our standard modular metric) at most \(mq/m^{10}=q/m^9\). Overall we get that if \(\sum \hat{s}_i c_i \mod{q}\) is in the interval \([0.4q, 0.6q]\) then \(\sum \hat{s}_i \tilde{c}_i \pmod{\tilde{q}}\) will be in the interval \([0.4q-100q/m^9, 0.6q+100q/m^9]\) which is contained in \([0.3\tilde{q},0.7\tilde{q}]\).

This completes the proof that our scheme can fit into the bootstrapping theorem (i.e., of Theorem 15.1), hence completing the description of the fully homomorphic encryption scheme.

Advanced topics:

Fully homomorphic encryption for approximate computation over the real numbers: CKKS

We have seen how a fully homomorphic encryption for a plaintext bit \(b\) can be constructed and we are able to evaluate addition and multiplication of ciphertexts as well as a NAND gate in the ciphertext space. One can also extend FHEENC scheme to encrypt a plaintext message \(\mu \in \Z_q\) and can evaluate multi-bit integer additions and multiplications more efficiently. Our next following question would be floating/fixed point operations. They are similar to integer operations, but we need to be able to evaluate a rounding operation following every computation. Unfortunately, it has been considered difficult to evaluate the rounding operation ensuring the correctness property. An easier solution is to assume approximate computations from the beginning and embrace errors caused by them.

CKKS scheme, one of the recent schemes, addressed this challenge by allowing small errors in the decrypted results. Its correctness property is more relaxed than what we’ve seen before. Now decryption does not necessarily be precisely the original message, and indeed, this resolved the rounding operation problem supporting approximate computation over the real numbers. To get more sense on its construction, recall that when we decrypt a ciphertext in the FHEENC scheme, we have \(\ensuremath{\mathit{CQ}}^\top s = bQ^\top s + e\) where \(\max |e_i| \ll \sqrt{q}\). Since \((Q^\top s)_1 \in (0.499q, 0.5001q)\), multiplying by this term places a plaintext bit near the most significant bits of the ciphertext where the plaintext cannot be polluted by the encryption noise. Therefore, we are able to precisely remove the noise \(e\) we added for the security. However, this kind of separated placement actually makes an evaluation of the rounding operation difficult. On the other hand, the CKKS scheme doesn’t clearly separate the plaintext message and noise in its decryption structure. Specifically, we have the form of \(c^\top s = m + e\) and the noise lies with the LSB part of the message and does pollute the lowest bits of the message. Note that this is acceptable as long as it preserves enough precision. Now we can evaluate rounding(i.e., rescaling in the paper) homomorphically, by dividing both a ciphertext \(c\) and the parameter \(q\) by some factor \(p\). The concept of handling ciphertexts with a different encryption parameter \(q'=q/p\) is already known to be possible. You can find more details on this modulus switching technique in this paper if you are interested. Besides, it is also proved that the precision loss of the decrypted evaluation result is at most one more bit loss compared to the plaintext computation result, which means the scheme’s precision guarantee is nearly optimal. This scheme offers an efficient homomorphic encryption setting for many practical data science and machine learning applications which does not require precise values, but approximate ones. You may check existing open source libraries, such as MS SEAL and HEAAN, of this scheme as well as many practical applications including logistic regression in the literature.

Bandwidth efficient fully homomorphic encryption GH

When we define homomorphic encryption in Definition 14.3, we only consider a class of single-output functions \(\mathcal{F}\). Now we want to extend the difinition to multiple-output function and consider how bandwidth-efficient the fully homomorphic encryption can be. More specifically, if we want to guarantee that the result of decryption is (or contains) \(f(x_1,\ldots,x_\ell)\), what will be the minimal possible length of the ciphertext? Let us first define the compressible fully homomorphic encryption scheme.

This definition is similar to the standard fully homomorphic encryption except an additional compression step. The bandwidth efficiency of a compressible fully homomorphic encryption is often described by the rate which is defined as follows:

The following theorem by Gentry and Halevi 2019 answers the earlier question, which states that the nearly optimal rate, say a rate arbitrarily close to 1, can be achieved.

Using fully homomorphic encryption to achieve private information retrieval.

Private information retrieval (PIR) allows the client to retrive the \(i\)-th entry of a database which has totally \(n\) entries without letting the server know \(i\). We only consider the single-server case here. Obviously, a trivial solution is that the server sends the entire database to the client.

One simple case of PIR is that each entry is a bit, for which the trivial solution above has the communication complexity being \(n\). Kushilevitz and Ostrovsky 1997 reduced the the complexity to be smaller than \(O(n^\epsilon)\) for any \(\epsilon>0\). After that, another work (Cachin et al. 1999) further reduced the complexity to \(polylog(n)\). More discussion about PIR and related FHE techniques can be found in Ostrovsky and Skeith 2007, Yi et al. 2013 and references therein.

One interesting observation is that fully homomorphic encryption can be applied to the single-server PIR via the following procedures:

• The client computes \(E_e(i)\) and sends it to the server.

• The server evaluates \(c=\ensuremath{\mathit{EVAL}}(f,E_e(i))\), where \(f(i)\) returns the \(i\)-th entry of the database, and sends it (or its compressed version \(c^*\)) back to the client.

• The client decrypts \(D_d(c)\) or \(D_d(c^*)\) and obtains the \(i\)-th entry of the database.

• Bandwidth efficient fully homomorphic encryption GH

Since there exists compressive fully homomorphic encryption scheme with nearly optimal rate, say rate arbitrary close to \(1\) (see Theorem 15.10), we can immediately get rate-\((1-\epsilon)\) PIR for any \(\epsilon\). (Note that this result holds only for database whose entries is quite large, since the rate is defined for circuits with sufficiently long output.) Prior to the theorem by Gentry and Halevi 2019, Kiayias et al. 2015 also constructed a PIR scheme with a nearly optimal rate/bandwidth efficiency. The application of fully homomorphic encryption to PIR is a fascinating field; not only limited to the bandwidth efficiency, you may be also interested in the computational cost. We refer to Gentry and Halevi 2019 for more details.

Comments

Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.

Compiled on 11/17/2021 22:36:18

Copyright 2021, Boaz Barak.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Produced using pandoc and panflute with templates derived from gitbook and bookdown.